Thể tích hình trụ là dạng bài tập cơ bản trong phần hình học của chương trình Toán lớp 12. Trong bài viết này, bạn sẽ được cung cấp công thức tính thể tích hình trụ cũng như các dạng bài tập cơ bản liên quan đến hình trụ.

Thế nào là hình trụ?
Định nghĩa về hình trụ
Cho một đường thẳng cố định là ∆, một đường thẳng d song song với ∆ và cách đường thẳng này một khoảng độ dài bằng R. Mặt tròn xoay sinh ra khi d xoay quanh ∆ gọi là mặt trụ tròn xoay, gọi tắt là mặt trụ. Cắt mặt trụ bằng hai mặt phẳng phân biệt cùng vuông góc với ∆ thu được hai giao tuyến là đường tròn. Phần mặt trụ và hai mặt giao tuyến tạo nên hình trụ. Hình trụ cùng với phần giới hạn bên trong nó gọi là khối trụ.
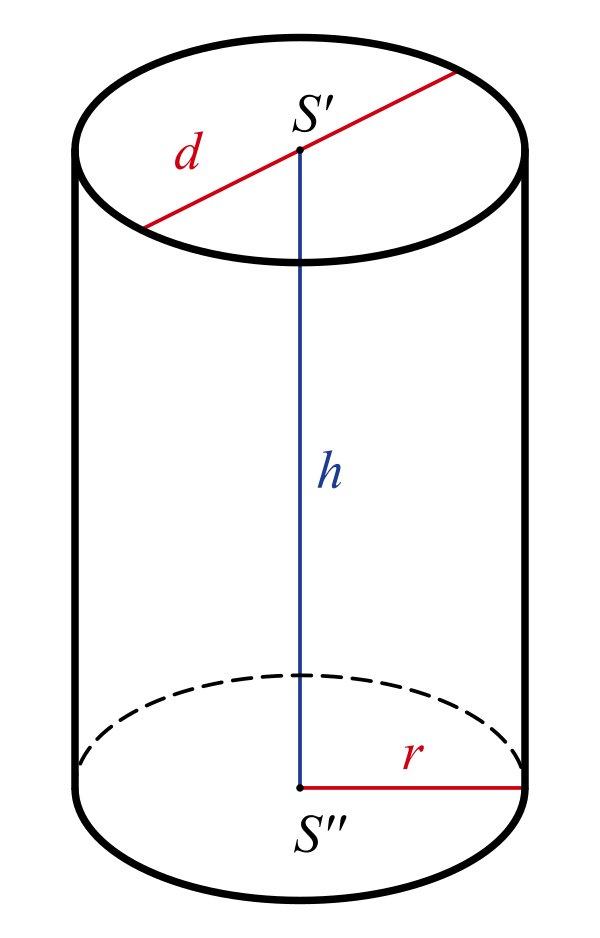
Đây là cách định nghĩa về mặt hình học trong môn Toán. Trên thực tế, người ta có cách hiểu đơn giản hơn. Hình trụ là hình có hai mặt đáy là hai hình tròn bằng nhau và vuông góc với trục giữa hình trụ.
Có rất nhiều những cách gọi khác nhau không thống nhất về hình trụ nên đôi khi có xảy ra một vài trường hợp nhầm lẫn. Hình trụ là cái tên thống nhất được dùng trong toán nhưng mọi người quen sử dụng các tên khác như lăng trụ, lăng trụ tròn, hình trụ tròn còn “hình trụ” nhiều khi lại được dùng làm tên gọi chung cho tất cả hình lăng trụ hay những khối đa diện.

Thể tích hình trụ
Có nhiều cách gọi khác nhau cùng để nói đến thể tích hình trụ như thể tích hình trụ tròn, thể tích hình lăng trụ tròn, hay thể tích hình trụ rỗng. Bài viết này sẽ thống nhất sử dụng cụm từ thể tích hình trụ.

Thể tích hình trụ là giới hạn của thể tích của lăng trụ đều nội tiếp hình trụ khi số cạnh đánh tăng lên vô hạn.
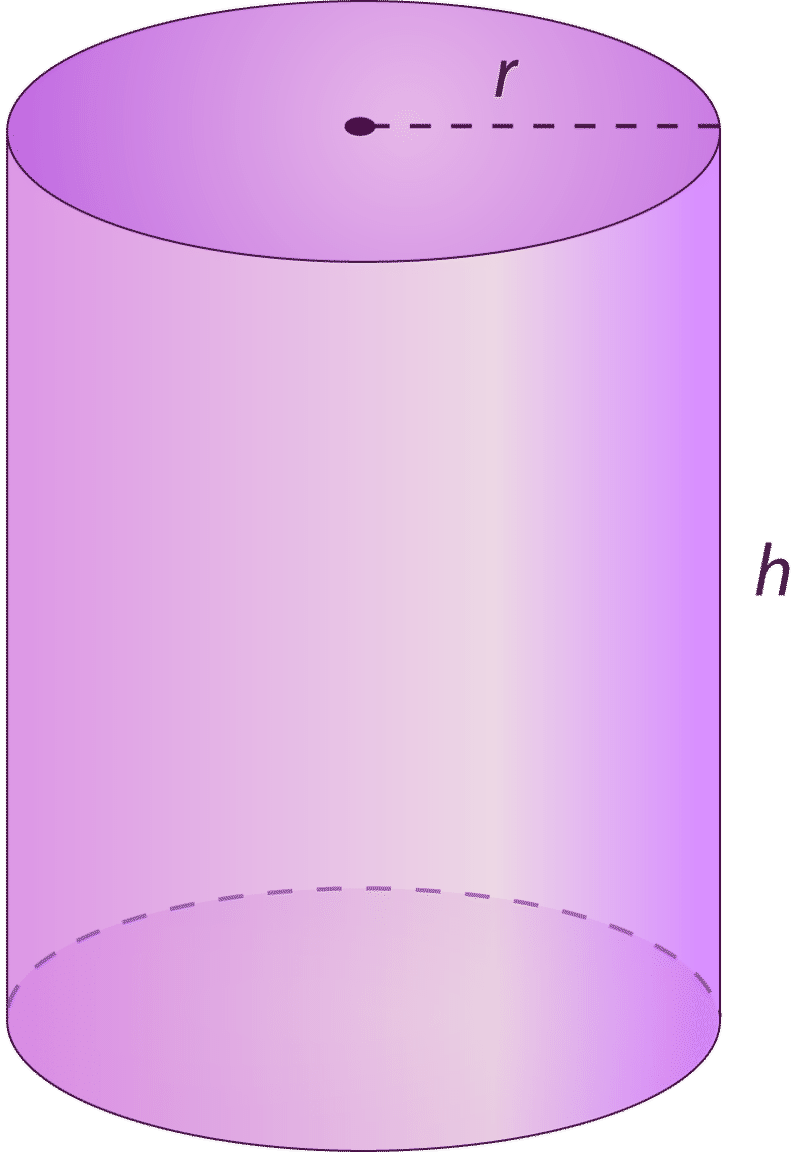
Công thức tính thể tích hình trụ
V = r2h
Trong đó:
- V là thể tích hình trụ
- r là bán kính mặt đáy hình trụ
- h là chiều cao hình trụ.
Cách tính thể tích hình trụ
Bước 1: Xác định bán kính đáy. Một số trường hợp đây là thông tin được cung cấp sẵn, còn trong những trường hợp còn lại được cho thông qua số đo đường kính hoặc từ những phép toán khác.
Bước 2: Xác định chiều cao hình trụ
Bước 3: Lắp những thông tin tìm được vào công thức tính thể tích hình trụ.
Các dạng bài tập liên quan đến tính thể tích hình trụ
Dạng bài tập cơ bản
Ví dụ 1: Lọ thủy tinh hình trụ có chiều cao 15 cm và bán kính đáy 5cm. Tính thể tích lọ thủy tinh.
Thể tích lọ thủy tinh: V = π r2h = 3.14 x 52 x 15 = 1 177.5 (cm3)

Ví dụ 2: Hình trụ có đường kính mặt đáy là 12 cm, chiều cao gấp 3 lần bán kính. Tính thể tích hình trụ đó.
Bán kính đây: r = d/2 = 12/ 2 = 6 (cm)
Chiều cao hình trụ: h = 3r = 3 x 6 = 18 (cm)
Thể tích hình trụ: V = π r2h = 3.14 x 62 x 18 = 2034.72 (cm2)
Ví dụ 3: Tính thể tích hình trụ biết chu vi đáy bằng 25 dm và chiều cao 6 dm.
Bán kính hình trụ: r = C/ 2π = 25 / (2 x3.14) ≈ 4 (dm)
Thể tích hình trụ: V = π r2h = 3.14 x 42 x 6 = 301.44 (dm3)
Ví dụ 4: Hình chữ nhật ABCD có AB = 10 cm, BC = 15 cm. Quay hình chữ nhật quanh cạnh BC. Tính thể tích hình trụ được tạo thành.
Thể tích hình trụ: V = π r2h = 3.14 x 102 x 15 = 4712.39 (cm3)
Ví dụ 5: Cho hình chữ nhật ABCD có tổng chiều dài AB và chiều rộng BC là 16 cm. Trong đó chiều dài gấp ba lần chiều rộng. Xoay hình chữ nhật quanh cạnh AB. Tính thể tích hình trụ được tạo thành.
Chiều dài hình chữ nhật AB = 16 / (3+1) x 3 =12 (cm)
Chiều rộng hình chữ nhật BC = 16 – 12 = 4 (cm)
Hình trụ có r = 4 cm và h = 12 cm
Thể tích hình trụ: V = π r2h = 3.14 x 42 x 12 = 602.88 (cm3)
=> Cùng học và thư giãn với list nhạc hay tại đây
Dạng bài tập nâng cao
Ví dụ 1: Hình chữ nhật ABCD có AB = 2BC. Quay hình chữ nhật quanh cạnh AB thu được hình trụ có thể tích V1. Quay hình chữ nhật quanh cạnh BC thu được hình trụ có thể tích V2. So sánh V1 và V2.
V1 = π r2h = π x BC2 x AB. Thay AB = 2BC, ta có: V1 = π x BC2 x 2BC = 2πBC3
V2 = π r2h = π x AB2 x BC. Thay AB = 2BC, ta có: V2 = π x 4BC2 x BC = 4πBC3
Như vậy, ta có: 2V1 = V2.

Ví dụ 2: Cho hình chữ nhật ABCD với AC = 10cm, AB = 6 cm. Quay hình chữ nhật quanh trục BC thu được hình trụ. Tính thể tích hình trụ đó.
Trong tam giác ABC: h = BC = AC2–AB2= 102–62 = 8 (cm)
Thể tích hình trụ: V = π r2h = 3.14 x 62 x 8 = 5425.92 (cm3)
Ví dụ 3: Cho hình trụ có chiều cao 7cm, thể tích bằng 175π. Một phẳng (P) song song với trục và cách trục 4 cm. Tính diện tích mặt cắt mà mặt phẳng này tạo nên.
Ta có V = π r2h = 175 π với h = 7 cm ? r = 5 cm
Trên mặt đáy, đặt tâm mặt đáy là O. (P) cắt mặt đáy bằng đoạn AB với A, B là hai điểm thuộc (O) bán kính 5 cm. OA = OB = 5 cm.
Khoảng cách từ O đến AB bằng khoảng cách từ (P) đến trục và bằng 4 cm. Kẻ đoạn OC vuông góc AB ? OC = 4 cm.
Trong tam giác AOC vuông tại C: AC = AO2–OC2= 52–42 = 3 cm
Chứng minh được ∆OCA = ∆OCB ?CB = CA = AB / 2 ? AB = 6 cm
Mặt cắt là hình chữ nhật có chiều dài bằng chiều cao hình trụ, chiều rộng là AB. Diện tích mặt cắt là S = 7 x 6 = 42 cm2.
Ví dụ 4: Hình trụ có bán kính R và chiều cao R3. Tính diện tích xung quanh, diện tích toàn phần và thể tích khối trụ.
Sxq = 2πrh = 2 x π x R x R3 = 23 π R2
Sđáy = πr2 = πR2
Stp = Sxq + 2 Sđáy = 23 π R2 + 2 πR2 = 2 (3 + 1) π R2
Thể tích hình trụ: V = π r2h = 3πR3
=> Các trường Đại học tốt nhất Hà Nội
=> Trò chơi dân gian hay cho bé
=> Một vé trở về tuổi thơ của thế hệ 8x, 9x với list nhạc audition